Binary To Decimal To Hexadecimal Converter

The binary to decimal to hexadecimal converter is an essential tool in digital electronics and computer science that enables seamless conversion between different number systems.

Binary numbers, consisting only of 0s and 1s, are the foundation of computer operations. The decimal system is our everyday counting method, while hexadecimal provides a more compact way to represent binary values using digits 0-9 and letters A-F.

Binary To Decimal To Hexadecimal Converter

Binary	Decimal	Hexadecimal	Process Description
10101100	172	AC	Groups of four, direct convert
11110000	240	F0	Power of two method
00111010	58	3A	Division by sixteen method
11000101	197	C5	Combined conversion
01011111	95	5F	Direct lookup method

Binary to Decimal to Hexadecimal Conversion Formula

Binary to Decimal:

To convert binary to decimal, multiply each digit by 2 raised to its position power (from right to left, starting at 0) and sum the results.

Formula: Decimal = Σ(bit × 2^position)

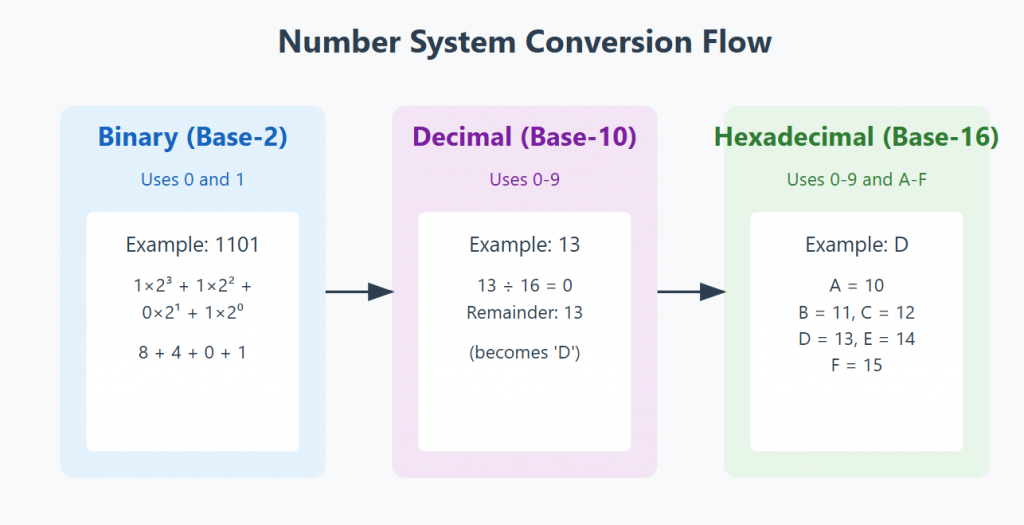
Example: Converting binary 1101

• 1 × 2^3 = 8
• 1 × 2^2 = 4
• 0 × 2^1 = 0
• 1 × 2^0 = 1
• Total = 13 decimal

Decimal to Hexadecimal:

To convert decimal to hexadecimal, repeatedly divide by 16 and track remainders in reverse order.

Example: Converting decimal 13 to hexadecimal

• 13 ÷ 16 = 0 remainder 13 (D)
• Result: D hexadecimal

How to Convert Binary to Decimal to Hexadecimal

Converting binary 11010110 to Decimal to Hexadecimal

Binary to Decimal:

• 1 × 2^7 + 1 × 2^6 + 0 × 2^5 + 1 × 2^4 + 0 × 2^3 + 1 × 2^2 + 1 × 2^1 + 0 × 2^0
• 128 + 64 + 0 + 16 + 0 + 4 + 2 + 0
• = 214 decimal

Decimal to Hexadecimal:

• 214 ÷ 16 = 13 remainder 6
• 13 ÷ 16 = 0 remainder 13 (D)
• Result: D6 hexadecimal

• First Step: Convert binary to decimal
  • Group binary digits
  • Apply the position-weight formula
  • Sum all values
• Second Step: Convert decimal to hexadecimal
  • Divide by 16 repeatedly
  • Convert remainders to hex digits
  • Read results bottom-up

Binary to Decimal to Hexadecimal Chart

Binary	Decimal	Hexadecimal
0000	0	0
0001	1	1
0010	2	2
0011	3	3
0100	4	4
0101	5	5
0110	6	6
0111	7	7
1000	8	8
1001	9	9
1010	10	A
1011	11	B
1100	12	C
1101	13	D
1110	14	E
1111	15	F

Converting Binary 111111110010 to Hexadecimal

• Group binary digits into sets of four: 1111 1111 0010
• Convert each group to decimal:
  • 1111 = 15 (F)
  • 1111 = 15 (F)
  • 0010 = 2 (2)
• Combine hexadecimal digits:
  • Result: FF2

References:

• IEEE Computer Society Digital Library: https://www.computer.org/education/standards

Related Conversion Tools :